Exemplos de calcúlos egípcios

Usando a formula de pitágoras

Exemplo 1: Sendo a,b e c as medidas dos comprimentos dos lados de um triângulo, indica, justificando, aqueles que são rectângulos: a) a = 6; b = 7 e c = 13; b) a = 6; b = 10 e c = 8. Resolução: "Se num triângulo as medidas dos seus lados verificarem o Teorema de Pitágoras então pode-se concluir que o triângulo é rectângulo". Então teremos que verificar para cada alínea se as medidas dos lados dos triângulos satisfazem ou não o Teorema de Pitágoras. a)            logo o triângulo não é rectângulo porque não satisfaz o Teorema de Pitágoras. b)            logo o triângulo é rectângulo porque satisfaz o Teorema de Pitágoras. Exemplo 2: Calcula o valor de x em cada um dos triângulos rectângulos: a)            b)                      Resolução: a) Aplicando o Teorema de Pitágoras temos:            b) Aplicando o Teorema de Pitágoras temos:              Exemplo 3: Calcula as áreas das seguintes figuras. a)            b)                     Resolução: a) b)                                 Exemplo 4: a) Qual era a altura do poste? Resolução:                       h = 4 + 5 = 9 Resposta: A altura do poste era de 9 m. b) Qual é a distância percorrida pelo berlinde.     Resolução:                          Resposta: A distância percorrida pelo berlinde é de:                             265 cm = 2,65 m.

Exercício 5: O Pedro e o João estão a «andar» de balancé, como indica a figura:   A altura máxima a que pode subir cada um dos amigos é de 60 cm. Qual o comprimento do balancé? Resolução do exercício 5: Pode-se aplicar o Teorema de Pitágoras, pois a linha a tracejado forma um ângulo de 90 graus com a "linha" do chão. Então vem: 1,8 m = 180 cm   Resposta: O comprimento do balancé é de aproximadamente 190 cm, isto é, 1,9 m. Exercício 6: A figura representa um barco à vela. 6.1.) Determina, de acordo com os dados da figura, os valores de x e y. Resolução do exercício 6: 6.1.) Aplicando o Teorema de Pitágoras, temos:

Exercícios sobre determinantes

    

      a) 64       b) 8       c) 0        d) 4        e) -64             RESPOSTA: D

                  

       a) 2 ou -2      b) 1 ou 3      c) -3 ou 5      d) -5 ou 3       e) 4 ou -4     RESPOSTA: A

                               

       a) não se define;     

       b) é uma matriz de determinante nulo;

       c) é a matriz identidade de ordem 3;

       d) é uma matriz de uma linha e uma coluna;

       e) não é matriz quadrada.                                     RESPOSTA: B

 

       a) duas linhas proporcionais;

       b) duas colunas proporcionais;

       c) elementos negativos;

       d) uma fila combinação linear das outras duas filas paralelas;     

       e) duas filas paralelas iguais.                                     RESPOSTA: D

       a) -9        b) -6       c) 3       d) 6        e) 9      RESPOSTA: E

      é igual a:

      a) 7         b) 8        c) 9       d) 10      e) 11     RESPOSTA: C

Números egípcios

Tabuleiro Xadrez

Monumentos Egipcios

cálculo do imc

Sistema de numeração egipcia

Cálculo de Massa Corporal

Matemática matrizes

Cálculo do índice de massa corporal (IMC)

     Você já deve ter ouvido falar do IMC, o índice de massa corporal. É uma medida que aponta o grau de obesidade de uma pessoa. Conhecendo o IMC, pode-se afirmar se ela está acima ou abaixo do peso ideal. É um índice que leva em consideração a altura e o peso (massa) do indivíduo. Sabemos que a obesidade já é considerada uma epidemia mundial pela Organização Mundial de Saúde, dessa forma, é importante saber como está o seu grau de obesidade. Mas o IMC também revela se a pessoa está abaixo do peso ideal, outro problema enfrentado pelas pessoas que buscam a qualquer preço ter um corpo magro, principalmente modelos, gerando um quadro de anorexia.

      Bem, como foi dito, o IMC é calculado considerando dois parâmetros: peso (massa) e altura da pessoa. Mas você sabe como ele é calculado? Há um modelo matemático (fórmula) que fornece o IMC quando se conhece o peso (em quilogramas) e a altura (em metros) de um indivíduo. Veja:

IMC = (peso) ÷ (altura)²

     Observe que o IMC é obtido fazendo o quociente (divisão) entre o peso da pessoa e o quadrado da altura.

     Assim, uma pessoa de 1,60 m de altura, com 51 kg de peso, terá um IMC de:

IMC = 51 ÷ (1,60)² = 51 ÷ 2,56 = 19,5

      A Associação Brasileira para o Estudo da Obesidade estabeleceu uma tabela que aponta o grau de obesidade de acordo com o IMC.

Abaixo de 18,5 à Você está abaixo do peso ideal
Entre 18,5 e 24,9 à Você está em seu peso normal
Entre 25 e 29,9 à Você está acima de seu peso (sobrepeso)
Entre 30 e 34,9 à Obesidade grau I
Entre 35 e 39,9 à Obesidade grau II
40 e acima à Obesidade grau III

     Se considerarmos o exemplo calculado anteriormente, como o IMC = 19,5, podemos afirmar que a pessoa está com o peso saudável.

Matriz

Curiosidades em torno do nome matriz

O pai do nome matriz

    Foi só há pouco mais de 150 anos que as matrizes tiveram sua importância detectada e sairam da sombra dos determinantes. O primeiro a lhes dar um nome parece ter sido Cauchy, 1826 : tableau ( = tabela ).
O nome matriz só veio com James Joseph Sylvester, 1850. Seu amigo Cayley, com sua famosa Memoir on the Theory of Matrices, 1858, divulgou esse nome e iniciou a demonstrar sua utilidade.

Por que Sylvester deu o nome matriz às matrizes ?

    Usou o significado coloquial da palavra matriz, qual seja: local onde algo se gera ou cria. Com efeito, via-as como "...um bloco retangular de termos... o que não representa um determinante, mas é como se fosse uma MATRIZ a partir da qual podemos formar varios sistemas de determinantes, ao fixar um número p e escolhar à vontade p linhas e p colunas..." ( artigo publicado na Philosophical Magazine de 1850, pag 363-370 ).

    Observe que Sylvester ainda via as matrizes como mero ingrediente dos determinantes. É só com Cayley que elas passam a ter vida própria e gradativamente começam a suplantar os determinantes em importância. 

Surgimento dos primeiros resultados da Teoria das Matrizes

    Costuma-se dizer que um primeiro curso de Teoria das Matrizes - ou de sua versão mais abstrata, a Algebra Linear - deve ir no mínimo até o Teorema Espectral. Pois bem, esse teorema e toda uma série de resultados auxiliares já eram conhecidos antes de Cayley iniciar a estudar as matrizes como uma classe notável de objetos matemáticos.

    Como se explica isso? Esses resultados, bem como a maioria dos resultados básicos da Teoria da Matrizes, foram descobertos quando os matemáticos dos séculos XVIII e XIX passaram a investigar a Teoria das Formas Quadráticas. Hoje, consideramos imprescindível estudar essas formas através da notacão e metodologia matricial, mas naquela época elas eram tratadas escalarmente.
Mostremos aqui a representação de uma forma quadrática de duas variáveis, tanto via notação escalar como com a mais moderna notação matricial:

q( x , y ) = a x 2 + 2b x y + c y 2	=	x	y	.	a	b	.	x
					b	c		y

    O primeiro uso implícito da noção de matriz ocorreu quando Lagrange c. 1790 reduziu a caracterização dos máximos e mínimos, de uma função real de várias variáveis, ao estudo do sinal da forma quadrática associada à matriz das segundas derivadas dessa função. Sempre trabalhando escalarmente, ele chegou à uma conclusão que hoje expressamos em termos de matriz positiva definida. Após Lagrange, já no século XIX, a Teoria das Formas Quadráticas chegou a ser um dos assuntos mais importantes em termos de pesquisas, principalmente no que toca ao estudo de seus invariantes. Essas investigações tiveram como subproduto a descoberta de uma grande quantidade de resultados e conceitos básicos de matrizes.

    Assim que podemos dizer que a Teoria das Matrizes teve como mãe a Teoria das Formas Quadráticas, pois que seus métodos e resultados básicos foram lá gerados. Hoje, contudo, o estudo das formas quadráticas é um mero capítulo da Teoria das Matrizes.
Observemos, ademais, que os determinantes em nada contribuiram para o desenvolvimento da Teoria das Matrizes.

Curiosidades Sobre o Egito Antigo

          As pirâmides egípcias foram construídas há mais de 3000 anos. A maior, localizada em Gizé, tem 2,3 milhões de blocos de pedra, alguns pesando nove toneladas, mas ninguém sabe como foram sobrepostos. A suposição mais divulgada aponta para milhares de pessoas a empurrarem os enormes blocos de pedra por rampas durante vários anos. Haja força ou será que foi pura matemática? 

          Agora, uma nova teoria afirma que a elevação das pedras - bem como dos obeliscos - foi conseguida recorrendo a papagaios de papel, então feitos com linho. As experiências para o demonstrar foram lideradas pela consultora californiana Maureen Clemmons.

         Foi em Junho de 1997 que Clemmons começou a usá-los no terreno para testar a sua teoria, quando tentou levantar, sem sucesso, um obelisco de 180 quilos diretamente ligado a um papagaio. No final desse ano, usando um "parafoil" (papagaio preso a viatura), conseguiu elevar um tronco de sequóia com 2,5 metros de comprimento. No ano seguinte, o obelisco inicial foi levantado na horizontal com uma asa delta e um "parafoil", depois de os papagaios ficarem destruídos na experiência.

         Em Maio deste ano, concluíram com sucesso um teste e, um mês depois, chamaram a   comunicação social para testemunhar a repetição da proeza. Dois homens, seis polias e um papagaio, ajudados por ventos de 25 a 30 quilômetros por hora, levantaram um obelisco com 3,4 toneladas de peso em 25 segundos. Como explica Clemmons, "o papagaio providenciava toda a tração e elevação para erguer o monumento, enquanto as polias davam vantagens mecânicas e os homens pilotavam o papagaio". Gomes da Cruz não tem dúvidas de ser possível usar papagaios para estas tarefas.

      Por que não existem relatos ou imagens dessas obras de engenharia com pessoas a manobrar os papagaios?

         Responde Clemmons. "Penso existirem imagens de egípcios a fazer voar papagaios mas não as soubemos interpretar", ou "Acho que as asas que vemos no topo dos antigos monumentos egípcios são, na realidade, representações de papagaios".

                           

OUTRA  TEORIA

         Os obeliscos eram colocados num buraco cheio de areia. Em seguida, através de um “tampo”, esvaia-se lentamente a areia branca para firmar o monumento.

 

Os egípcios na:

   Astronomia - Foi a mais importante das ciências desenvolvidas pelos egípcios. Impulsionados pela necessidade de medir o tempo do início e do fim das cheias do Nilo, para isso eles fizeram um calendário, que dividia o ano em 365 dias e três estações: cheia, inverno e verão. Inventaram o relógio de sol, os obeliscos, e o de água. Traçaram mapas celestes, situaram os pontos cardeais e quem sabe muito mais.

     Matemática - Lançaram os fundamentos da Aritmética e da Geometria. Inventaram a soma, a subtração e a divisão sem nem um tipo de símbolo para representar o zero, constituíram o sistema decimal. Não sabiam multiplicar. Determinaram triângulos e retângulos.

    A matemática era usada principalmente na construção dos templos, pirâmides e outras grandes obras, como os diques e as barragens, que impediam as cheias do Nilo. Foram as mesmas cheias desse rio que levaram os egípcios a desenvolverem a geometria, que servia para dividir as terras, pois quando as águas baixavam e as divisões das propriedades sumiam era necessário reconhecê-las novamente. Eles sabiam medir áreas de triângulos, retângulos e hexágonos, e o volume de cilindros e pirâmides. Como se vê, todas as forças da natureza sempre estiveram muito presentes na vida dos egípcios, e isto mostra porque eles as idolatravam tanto, dando muito poder para quem as propagavam como divinas (sacerdotes e faraós), e criaram uma cultura em torno de si mesmas, fazendo com que um povo inteiro vivesse para elas e em torno delas.

    A medicina era muito desenvolvida, embora os conhecimentos médicos ficassem nas mãos de poucas pessoas. Os egípcios praticavam operações, incluindo a perfuração do crânio a fim de diminuir a pressão no cérebro, conheciam uma grande variedade de doenças e, além disso, conheciam a importância do coração.

       A escrita egípcia, inicialmente denominada hieroglífica, era composta de pequenas figuras que representavam as coisas. Essa era a escrita sagrada, que se encontrava nos túmulos e templos. Posteriormente ela foi simplificada, dando origem a escrita hierática, que era usada pelos sacerdotes nos textos sagrados. E ainda surgiu uma terceira escrita, muito mais simples, usada pelos escribas e pela população em geral. Os hieróglifos foram decifrados por um francês chamado Champollion. Entender sinais tão complicados só não era mais difícil do que descobrir o mistério das pirâmides.                  

      Por isso, Champollion teve que contar com uma pequena ajuda. Em 1779, os exércitos de Napoleão trouxeram do Egito a pedra da Roseta:  um pedaço de basalto negro onde estava gravado um texto em grego, em hieróglifos e em demótico. Está última forma era uma escrita egípcia mais simplificada, empregada nos papiros administrativos e literários. Na versão grega, o texto era um decreto baixado por Ptolomeu V em 196 a.C. Os dois outros poderiam ser traduções. Por ordem de Napoleão Bonaparte a estela foi reproduzida e litografada e várias cópias enviadas a diversos especialistas em línguas mortas.Em 1807, Jean-François Champollion aceitou o desafio de decifrar. A partir dos nomes próprios do texto grego, ele comparou os outros dois textos até descobrir certas semelhanças. Foram necessários quatorze anos para o professor dispor de algumas chaves para entender o enigma: No total, foram.vinte e três anos desde a data de sua descoberta até  Champollion pudesse decifrar integralmente o seu conteúdo. Enfim, a pedra da Roseta e as inscrições de outros monumentos egípcios revelaram grandes segredos.

A escrita é considerada como o maior tesouro deixados pelos egípcios, pois..

                                                 .

 Bastam olhos que saibam ler para ressuscitar todo o   conhecimento.

A história do xadrez

     O Xadrez é um jogo tão antigo que, durante todos os anos de sua existência, várias foram as histórias associadas a sua origem.

     A primeira história que se é contada mundialmente se passa na Índia. Havia uma pequena cidade chamada Taligana, e o único filho do poderoso rajá foi morto em uma sangrenta batalha. O rajá entrou em depressão e nunca havia conseguido superar a perda do filho. O grande problema era que o rajá não só estava morrendo aos poucos, como também estava se descuidando em relação ao seu reino. Era uma questão de tempo até que o reino caísse totalmente.

     Vendo a queda do reino, um brâmane chamado Lahur Sessa, certo dia foi até o rei e lhe apresentou um tabuleiro contendo 64 quadrados, brancos e pretos, além de diversas peças que representavam fielmente as tropas do seu exército, a infantaria, a cavalaria, os carros de combate, os condutores de elefantes, o principal vizir e o próprio rajá.

     O sacerdote disse ao rajá que tal jogo poderia acalmar seu espírito e que sem dúvida alguma, iria curar-se da depressão. De fato, tudo o que o brâmane disse acontecera, o rajá voltou a governar seu reino, tirando o a crise de seu caminho.

     Era inexplicável como aquilo tudo aconteceu, sendo um único tabuleiro com peças o responsável por tirar a tristeza do rajá. Como recompensa, o brâmane foi agraciado com a oportunidade de pedir o que quisesse. Logo de primeira, ele recusou tal oferta, pois achava que não fosse merecedor de tal proposta, mas mediante insistência do rajá, ele fez um simples pedido. O brâmane pediu simplesmente um grão de trigo para a primeira casa do tabuleiro, dois para a segunda, quatro para a terceira, oito para a quarta e assim sucessivamente até a última casa. O rajá chegou a achar graça, tamanha a ingenuidade do pedido.

     Entretanto, o humilde pedido do brâmane não era tão humilde assim. Após fazerem vários cálculos de quanto trigo eles teriam que dar para ele, descobriram que seria necessário toda a safra do reino por incríveis dois mil anos para atender ao pedido do sacerdote. Impressionado com a inteligência do brâmane, o rajá o convidou para ser o principal vizir (espécie de ministro, conselheiro do rajá) do reino, sendo perdoado por Sessa de sua grande dívida em trigo.

     Na verdade, o que o brâmane apresentou para o rajá não foi o jogo de xadrez, foi a chaturanga, uma das principais variantes do jogo de xadrez moderno.

     Outra grande possibilidade que se apresenta em diversas histórias sobre a origem do Xadrez, é que Ares, o deus da guerra, teria criado um tabuleiro para testar suas táticas de guerra (que eram bem limitadas, pois Ares nunca foi conhecido por ter tática nas suas batalhas, ele era simplesmente agressivo, atacando sem precisão alguma na maioria das vezes). Entretanto, cada peça do tabuleiro representava uma parte do seu exército, e assim foi, até que Ares teve um filho com uma mortal, e passou para ele os fundamentos do jogo. A partir de então, o jogo teria chegado ao conhecimento dos mortais.

     É sabido que entre 1450 e 1850, o Xadrez começou a ter mudanças visíveis em relação ao que conhecemos hoje em dia. Foi nesse período que diversas peças ganharam movimentos que conhecemos atualmente, claro, todos esses movimentos e peças tendo como origem a Chaturanga.

     O elefante (o antecessor do moderno bispo) somente podia mover-se em saltos por duas casas nas diagonais. O vizir (o antecessor da dama) somente uma casa nas diagonais. Os peões não podiam andar duas casas em seu primeiro movimento e não existia ainda o roque. Os peões somente podiam ser promovidos a vizir, que era a peça mais fraca, depois do peão, em razão da sua limitada mobilidade.

     As regras do Xadrez que conhecemos hoje começaram a ser feitas em 1475, só não se sabe ao certo onde ocorreu esse início. Alguns historiadores divergem entre Espanha e Itália.

     Foi neste período que os peões ganharam a mobilidade que conhecemos hoje em dia, que se resume em mover-se duas casas no seu primeiro movimento e tomar outros peões en passant. Nessa época também foram definido os novos movimentos dos bispos e da rainha e, o mais importante, a rainha tornou-se a peça mais importante do jogo, sendo a única capaz de se movimentar para qualquer lado e avançar ou recuar quantas casas quiser. Os movimento das demais peças, juntamente com o resto das regras que englobam todo o Xadrez, só foram formalmente modificadas no meio do século XIX, e tais regras ainda se mantêm até hoje.

Garoto de 16 anos cursa ensino médio e mestrado em matemática

Daniel Rocha pode pegar diploma só depois de concluir graduação.
Filho de professor, jovem mora no Rio de Janeiro e estuda no Impa.

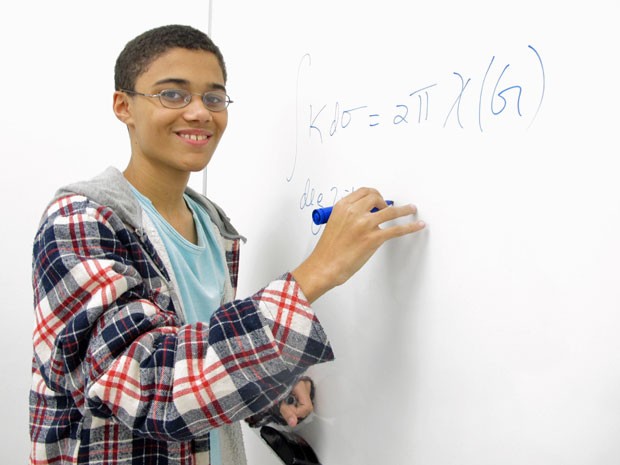
    Quando tinha 11 anos, Daniel Santana Rocha foi acompanhar o pai em um curso de matemática para professores e surpreendeu a sala de aula ao resolver um exercício que parecia indecifrável por todos. Foi para lousa e mostrou a resolução para orgulho do pai, que também não tinha conseguido chegar na resposta do problema. Hoje aos 16, a presença de Daniel no curso de mestrado em matemática pura no Instituto Nacional de Matemática Pura Aplicada (Impa), instituição que reúne a excelência em matemática do país no Rio de Janeiro, não causa mais espanto.

         Segundo o pai de Daniel, os docentes do Impa não veem mais o filho como criança. “Eles já esqueceram isso, já se habituaram.” Daniel não foi o único aluno a entrar no Impa sem ao menos ter completado do ensino médio. Quem puxou a fila foi o professor Carlos Gustavo Tamm de Araujo Moreira, o Gugu, que fez doutorado e leciona na instituição, mas ingressou em março de 1988 quando tinha 15 anos. Aos 17 já tinha concluído a graduação e o mestrado.

Daniel também disputa olimpíadas desde o ensino fundamental. Por muito pouco não passou na seletiva para compor a equipe que vai disputar a internacional na Colômbia. No histórico acumula pelo menos 20 medalhas em competições nacional e internacionais.

“Meu pai sempre me ensinou mais matemática do que o colégio. Aos 12, já sabia toda a matéria do ensino médio, mas não sou gênio, todo mundo pode aprender. Acontece que o jeito que ensinam no ensino médio você não aprende o que é de verdade”, afirma.

Fernando conta que o filho estuda mais do que ele, que ainda não conseguiu fazer um mestrado. “Quando tenho dúvidas em matemática, ligo para ele. Outros professores também fazem isso. Ele é bom para ensinar. Eu também dou aulas particulares, nunca levo o Daniel junto porque se eu faço isso, perco o aluno.”